Optimal Substructures in Spatial Reduction Models

Jordan Smith and Soren Larson

Abstract

Modeling in atmospheric transport, astrophysics, diagnostics, genomics, materials science, engineering, and a variety of other systems face a significant constraint in optimizing the distribution of computing power and process sequences in order to appropriately represent forward and inverse model states. Once data is obtained, a vast amount of computational power is necessary to study these relationships. Improved methods of appropriately discerning optimal substructures have the potential to significantly reduce required computational resources while preserving a high degree of overall model accuracy.

Dimension reduction has been well-received as a means of producing cost-effective representations of large-scale systems. In order to reduce the total number of calculations necessary to model a time series in high-dimensional space, methods of extrapolation are commonly used by practitioners as a means by which to reduce computational expense. In these instances, the discretization of partial differential equations (PDEs) aids in optimal control, probability analysis, and inverse problems requiring multiple iterations of system simulation. This iterative approach necessitates that the reduced model produce an accurate representation of the system across a large number of parameters. Dynamic programming has contributed to these model acceleration methods through the isolation of identical problems normally solved many times by the model, known as overlapping sub-problems.

An illustration of the advantages afforded by the implementation of select methods described is simulated using an atmospheric chemical transport application. A global atmospheric model is constructed using empirical time-series data from the Emissions Database for Global Atmospheric Research (EDGAR), and the concentration of chemical species is determined using inverse modeling. In order to improve computation performance, the Jacobian matrix is optimized using a quasi-Newton variable metric algorithm. The model then produces a representation of chemical species concentration in different hemispheres and atmospheric layers across time at  significantly reduced computational cost.

rtreeviz rtree

Use of a Jacobian matrix and spatial reduction both compartmentalize a given model into two separate regions, with independent variables being solved at each time step and dependent variables either relying upon a system of PDEs or being identified as overlapping sub-problems and subsequently eliminated entirely by dynamic programming. As one or more regions of the system run the model at a normal speed (“fast”) using conventional modeling methods and solving the full mechanism of all equations , other sections run pre-specified components of the model at an accelerated speed using extrapolation (“slow”). These functions both lead to PDEs, requiring numerical analysis techniques to arrive at an optimal solution. The separate sections are then paired in order to extrapolate basic knowledge of the system without having to run every component of the model, substantially reducing computational strain and overall run-time.

The most pronounced drawback of spatial reduction models is that the nature of extrapolation produces additional error, and can lead to highly inaccurate results over the course of the model due to compounding. When applied to models involving time series in high dimensional space, the error produced by extrapolation is often too high to justify the computational savings. For this reason, successful implementation of spatial reduction models has been limited to those with an advanced understanding of the underlying system, in this case primarily geophysicists with atmospheric transport modeling expertise. Improvements in constraining this error without excessive manual adjustments to the model can be achieved by isolating optimal substructures and introducing a trainer.

Application

A large-scale system with some dynamical substructures is desirable for the purposes of examining the range and degree of impact of the algorithm framework relative to both basic extrapolation and standard computation methods. Though generally applicable to many natural sciences systems, this analysis shall focus upon a global atmospheric modeling application due to the expansive size and diverse nature of the system, constant geophysical laws, variety of chemical species, recognizable regions, presence of overlapping substructures, and ease of discretization.

This simulation considers the long-lived greenhouse gas \text{N}_2\text{O}. The radiative forcing of \text{N}_2\text{O} is the one of the largest of all greenhouse gases, third only behind \text{CO}_2 and \text{CH}_4. In the case of a tropospheric species harmful to the human respiratory system, point source attribution is essential to maintaining or improving public health in the affected area.

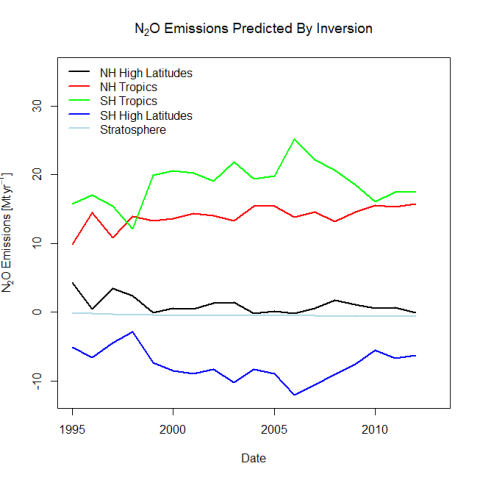
Atmospheric concentration of \text{N}_2 \text{O} is estimated using a five box model with linear transport and removal that has been fit to a time series of observations. In order to evaluate model performance, chemical impulses were used to simulate a change in emissions during periods which would not have ordinarily been predicted by an extrapolation method.

fig7fig6

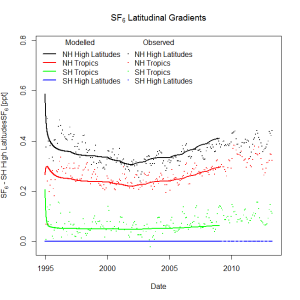
Linear transport coefficients were optimized by in-situ concentration observations of \text{SF}_6, which was selected because it is known to be correlated to concentrations of \text{N}_2 \text{O}. This was deliberate not simply in the hope of ensuring an accurate final model output, but also due to the fact that the two species likely have a variety of overlapping sub-problems and are less likely to diverge significantly during accelerated extrapolation. Transport between boxes in the model is fully constrained by four parameters (stratospheric turnover time, interhemispheric exchange time, intrahemispheric exchange time, and the fraction of stratospheric air extruded into the Northern Hemisphere), global mass conservation, and the assumption that the mass of each box remains constant in time.

The Jacobian is ideal in dynamical systems for which and for inverse functions, and can be plainly written as (J_{F^-1})(F(p)) = [(J_F)(p)]^{-1}. Given that the Jacobian generalizes the gradient of a scalar-valued function of multiple variables, if a function is differentiable at point p, the function need not be differentiable for the Jacobian to be accurately defined due to the fact that only partial derivatives are required. Therefore the Jacobian would still give the coordinates of the derivative, p'.

The Jacobian relates to a first order Taylor expansion f(x) = f (p) + f'(p) (x-p) +o(x-p) in that p is a point in \mathbb{R}^n, and given that F is differentiable at p, p' = J_F (p), enabling a linear map to approximate F in the neighborhood of p s.t. the following holds, where o= x \rightarrow p and the distance between \text{\bf x} and \text{\bf p} = || \text{\bf x} -\text{\bf p}||:

F(\text{\bf x}) = F (\text{\bf p}) + J_F (\text{\bf p}) (\text{\bf x} - \text{\bf p}) + o (||\text{\bf x}-\text{\bf p}||)

For these reasons, the Jacobian is used commonly in global physical sciences modeling. In the application used for this project, the first and second order derivatives of independent variables are known. In such scenarios, most mainstream atmospheric models simply use the Jacobian to create a PDE matrix, solve the inverse problem, and adjust parameters as necessary to obtain a highly accurate fit.

After an initial estimate of the parameter values, the Jacobian matrix is constructed, and the standard objective function \phi = || d-Gm||_{2}^{2} is minimized in order to solve the inverse problem. The gradient can  then be expressed in a manner equivalent to ordinary least squares:

\nabla_m \phi = G^T Gm -G^T d =0 \Rightarrow G^T Gm = G^T d \Rightarrow m = (G^TG)^{-1}G^T d

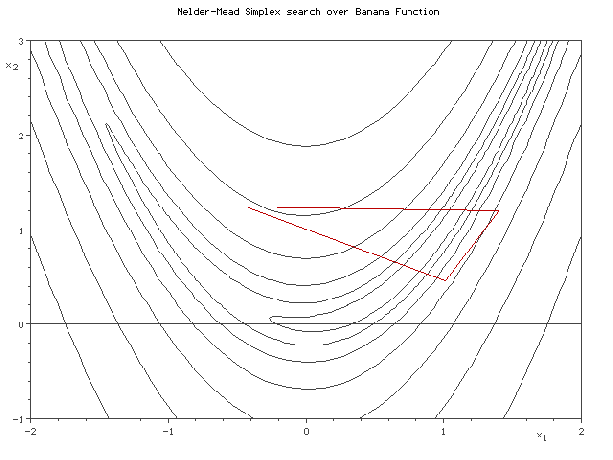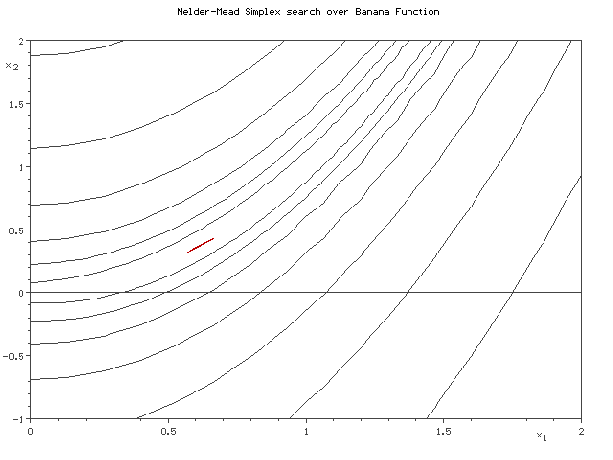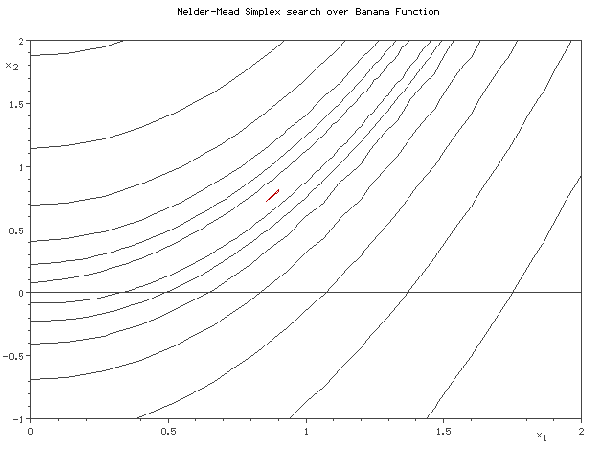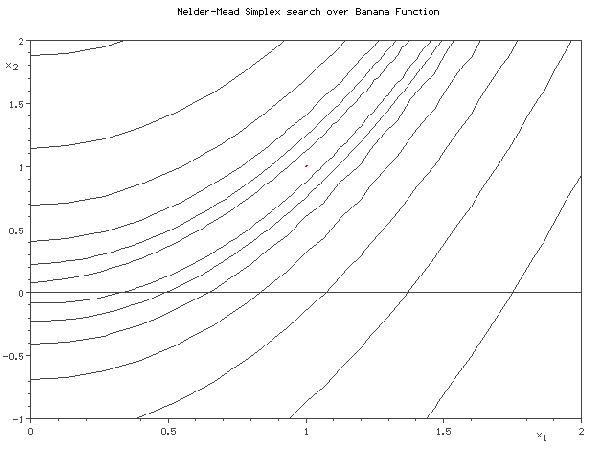
Here the Jacobian itself is performing a reduction function in that the configuration of partial derivatives creates a system in which dependent variables are already being partitioned as overlapping sub-problems and computational resources are not being expended upon optimizing them. A Nelder-Mead algorithm is then implemented in order to find the optimal initial starting chemical species concentration in each of the atmospheric layers.

Nelder_Mead1

Given the inverse has now been established and the optimal parameters are known, the model is run and compared to empirical data from the Intergovernmental Panel on Climate Change (IPCC). The values are found to be consistent for \text{SF}_6 concentrations, and therefore the transport values are known to be accurate.  The system is then applied to forcing \text{N}_2 \text{O} values, and the model-predicted figures again align with EDGAR observations and third party calculations.

fig14

Evaluating means of reducing computational expense, a scenario is presented in which no in-depth familiarity with the system is assumed. A trainer and Greedy algorithm are then used in a vector autoregression (VAR) scenario in an attempt to reduce computational expense.

Findings

The inverse model accurately reflects the time-series concentrations of \text{N}_2 \text{O}, and therefore optimization of the transport parameters and initial concentrations have been solved for both chemical species. Implementation of VAR and the Greedy algorithm perform as expected, though the exercise highlighted the fact that in most scenarios, the analyst must have a high degree of familiarity with the technical aspects of the system in order to observe and remedy any anomalies in the data or model trajectory.

fig5fig4

Recommendations for spatial reduction techniques going forward include increased specification in trainers, ranking/weighting depending upon past performance and known correlations or other period/parameter-specific relationships, use of partial derivatives as a prompt to sample from true observations in areas of decreased stability, and improved means of isolating optimal substructures.

Leave a comment